Detect cycle in directed graph
Note: Try to solve this task in O(m + n) or O(n) time, where n is a number of vertices and m is a number of edges, since this is what you'll be asked to do during an interview.
In a multithreaded environment, it's possible that different processes will need to use the same resource. A wait-for graph represents the different processes as nodes in a directed graph, where an edge from node i to node j means that the node j is using a resource that node i needs to use (and cannot use until node j releases it).
We are interested in whether or not this digraph has any cycles in it. If it does, it is possible for the system to get into a state where no process can complete.
We will represent the processes by integers 0, ...., n - 1. We represent the edges using a two-dimensional list connections. If j is in the list connections[i], then there is a directed edge from process i to process j.
Write a function that returns True if connections describes a graph with a directed cycle, or False otherwise.
Example
- For
connections = [[1], [2], [3, 4], [4], [0]], the output should behasDeadlock(connections) = true.
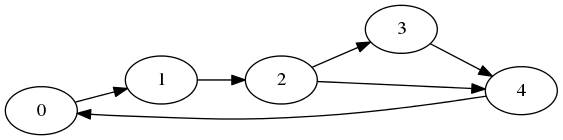
This graph contains a cycle.
- For
connections = [[1, 2, 3], [2, 3], [3], []], the output should behasDeadlock(connections) = false.
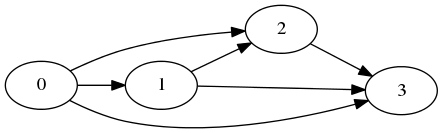
This graph doesn't contain a directed cycle (there are two paths from 0 to 3, but no paths from 3 back to 0).
Input/Output
[execution time limit] 3 seconds (java)
[input] array.array.integer connections
A representation of the graphs edges.
connection.lengthis the number of vertices. Ifjis in the listconnections[i], then there is a directed edge from processito processj.Guaranteed constraints:
1 ≤ connections.length ≤ 500,0 ≤ connections[i][j] < connections.length,connections[i][j] ≠ connections[i][k]forj ≠ k,i not in connections[i].[output] boolean
- Return
Trueifconnectionsdescribes a graph with a directed cycle, orFalseotherwise.
- Return