Efficient Road Network
Once upon a time, in a kingdom far, far away, there lived a King Byteasar III. As a smart and educated ruler, he did everything in his (unlimited) power to make every single system within his kingdom efficient. The king went down in history as a great road builder: during his reign a great number of roads were built, and the road system he created was the most efficient during those dark times.
When you started learning about Byteasar's III deeds in your history classes, a creeping doubt crawled into the back of your mind: what if the famous king wasn't so great after all? According to the most recent studies, there were n cities in Byteasar's kingdom, connected by two-way roads. You managed to get information about these roads from the university library, so now you can write a function that will determine whether the road system in Byteasar's kingdom was efficient or not.
A road system is considered efficient if it is possible to travel from any city to any other city by traversing at most 2 roads.
Example
For
n = 6androads = [[3, 0], [0, 4], [5, 0], [2, 1], [1, 4], [2, 3], [5, 2]]the output should be
efficientRoadNetwork(n, roads) = true.Here's how the road system can be represented:
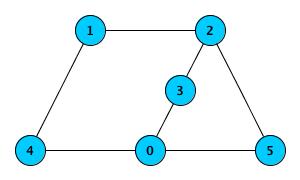
For
n = 6androads = [[0, 4], [5, 0], [2, 1], [1, 4], [2, 3], [5, 2]]the output should be
efficientRoadNetwork(n, roads) = false.Here's how the road system can be represented:
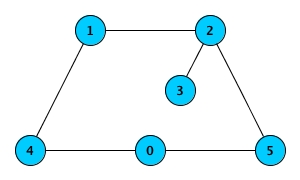
As you can see, it's only possible to travel from city
3to city4by traversing at least3roads.
Input/Output
[execution time limit] 3 seconds (java)
[input] integer n
The number of cities in the kingdom.
Guaranteed constraints:
1 ≤ n ≤ 250.[input] array.array.integer roads
Array of roads in the kingdom. Each road is given as a pair
[cityi, cityj], where0 ≤ cityi, cityj < nandcityi ≠ cityj. It is guaranteed that no road is given twice.Guaranteed constraints:
0 ≤ roads.length ≤ 35000,roads[i].length = 2,0 ≤ roads[i][j] < n.[output] boolean
trueif the road system is efficient,falseotherwise.