Tree Diameter

-
https://app.codesignal.com/interview-practice/task/Sby2j4SHqDncwyQjh

You got sick because of walking in the woods at night, and have to spend a week at home without going out. Looking out of the window at the nearby woods you're wondering if there is anything you don't yet know about them. Suddenly you see a beautiful and very tall tree you haven't seen before. Since you have nothing to do, you decide to examine its structure and draw it in your notebook.

You became so exited about this new tree that your temperature went up, so you were forced to stay in bed. You can't see the tree from your bed, but luckily you have it drawn down. The first thing you'd like to find out about is the tree height. Looking at your drawing you suddenly realize that you forgot to mark the tree bottom and you don't know from which vertex you should start counting. Of course a tree height can be calculated as the length of the longest path in it (it is also called tree diameter). So, now you have a task you need to solve, so go ahead!

Example

For n = 10 and

tree = [[2, 5], [5, 7], [5, 1], [1, 9], [1, 0], [7, 6], [6, 3], [3, 8], [8, 4]]

the output should be treeDiameter(n, tree) = 7.

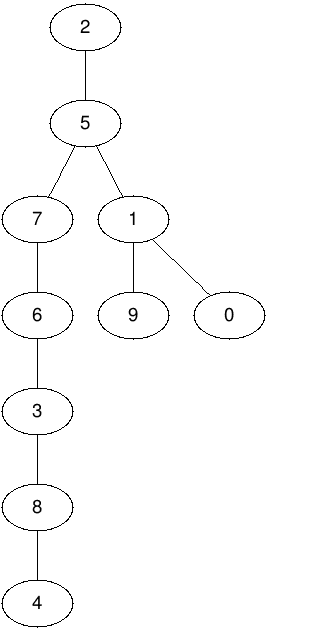
The longest path is the path from vertex 4 to one vertex 9 or 0.

Input/Output

  • [execution time limit] 3 seconds (java)

  • [input] integer n

    The number of vertices in the structure you drew in your notebook.

    Guaranteed constraints:
    1 ≤ n ≤ 104.

  • [input] array.array.integer tree

    Edges of the tree. tree[i] for each valid i contains two elements and represents an edge that connects tree[i][0] and tree[i][1].
    It is guaranteed that given graph is a tree, i.e. it is connected and has no cycles.

    Guaranteed constraints:
    tree.length = n - 1,
    tree[i].length = 2,
    0 ≤ tree[i][j] < n.

  • [output] integer

    • tree diameter of the given tree.
---
Related problems
---