1339. Maximum Product of Splitted Binary Tree

https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

 

Example 1:

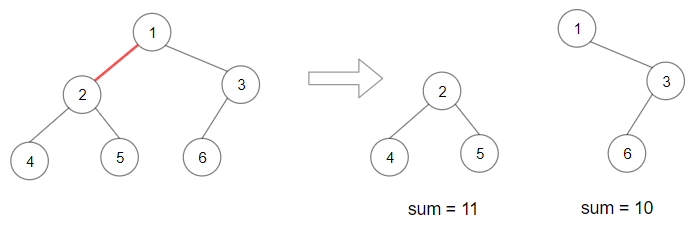
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

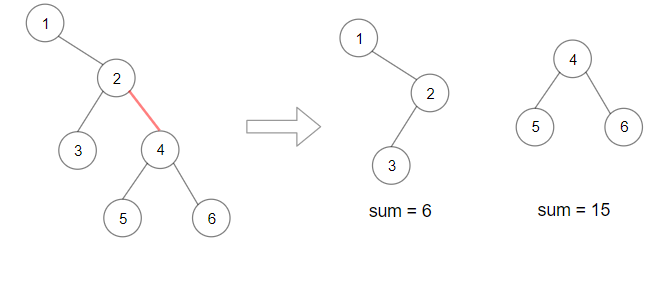
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

 

Constraints:

• Each tree has at most 50000 nodes and at least 2 nodes.
• Each node's value is between [1, 10000].

---

Intuition

Compute total of all node values

At each node - find sum of subtree rooted at that node

Calculate product of sum(subtree) * (total - sum(subtree))

Track max product as long ans

---

Time - O(N)

Space - O(N) - word case for skewed tree

---